为了你好。（咦？）
原文链接：https://blogs.msdn.microsoft.com/oldnewthing/20040218-00/?p=40563
Endpoint-exclusive RECTs and lines are much easier to work with.
（简而言之，）排除了终端端点的矩形（RECT）处理起来更容易。
For example, the width of a rectangle is right – left, and its height is bottom – top. If rectangles were endpoint-inclusive, then there would be annoying +1’s everywhere.
例如，某个矩形的宽度是右端点值减左端点值，其高为下端点值减上端点值，如果矩形包含终端端点，那么到处都会多1个像素，而这是挺讨厌的。
End-point exclusive rectangles also scale properly.
排除终端端点的矩形也有利于正确地进行缩放。
For example, suppose you have two rectangles (0,0)-(100,100) and (100,100)-(200,200). These two rectangles barely touch at the corner. Now suppose you magnify these rectangles by 2, so they are now (0,0)-(200,200) and (200,200)-(400,400). Notice that they still barely touch at the corner. Also the length of each edge doubled from 100 to 200.
举例来说，现在有两个矩形(0,0)-(100,100)和(100,100)-(200,200)，这两个矩形在两个顶角处刚刚好碰在一起。现在假设将这两个矩形放大2倍，现在两个矩形就分别是(0,0)-(200,200)和(200,200)-(400,400)了，可以注意到这两个矩形仍然在顶角处刚刚好碰在一起，二者的每边边长也从100加倍到了200。
Now suppose endpoints were inclusive, so the two rectangles would be (0,0)-(99,99) and (100,100)-(199,199). Now when you double them, you get (0,0)-(198,198) and (200,200)-(398,398). Notice that they no longer touch any more because (199,199) is missing. Note also that the length of the side of the square is now 199 pixels instead of 200.
现在假设矩形的计算包含了端点，那这两个矩形就会变成(0,0)-(99,99)和(100,100)-(199,199)，在这种情况下将其加倍放大，获得的结果将是(0,0)-(198,198)和(200,200)-(398,398)。请注意此时两个矩形的顶角不再碰在一起，因为(199,199)处的像素点消失了，而且矩形的边长现在也是199像素而不是（正确的）200像素。
Similar problems occur if you need to do subpixel computations.
类似的问题在需要进行子像素计算时也会发生。
“But that’s silly — who ever does magnification or subpixel computations?”
『可是这听起来挺傻的，有谁会整天做这种放大和子像素计算的事情啊？』
Well, magnification is used more than you think. In addition to the obvious things like zooming in/out, it’s also used in printing (since printers are 300dpi but the screen is usually much lower resolution) and in GDI mapping (ScaleWindowExtEx, StretchBlt). And subpixel computations are used in anti-aliasing.
其实吧，像上面这种放大计算比你想象的场合要多。除了显而易见的（屏幕显示）放大/缩小之外，类似的事情在打印时（鉴于打印机通常的分辨率是300dpi，但屏幕的分辨率通常远低于此数值）和GDI映射（ScaleWindowExtEx、StretchBlt等）。此外，子像素计算在抗锯齿等功能中也很常见。
With apologies to Alvy Ray, I think the best way to interpret this is to view pixels as living between coordinates, not at them. For example, here’s a picture of the pixel that lives between (10,10) and (11,11). (In other words, this pixel is the rectangle (10,10)-(11,11).)
在这里对Alvy Ray说声抱歉（译注：链接指向的页面已无法访问，所以并不知道Raymond在为啥道歉），我想解释这个问题最好的方式是将像素视为居于像素之间，而不是之上。例如，下图示意了一个居于坐标(10,10)和(11,11)之间的像素。（亦即，该像素等同于矩形(10,10)-(11,11)）
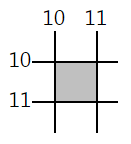
With this interpretation, the exclusion of the endpoint becomes much more natural. For example, here’s the rectangle (10,10)-(13,12):
基于这种解释，（矩形）对于终端端点的排除就显得更为自然了。例如，下图示意的是矩形(10,10)-(13,12)：
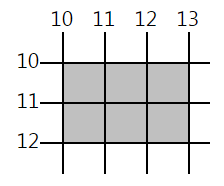
Observe that this rectangle starts at (10,10) and ends at (13,12), just like its coordinates say.
观察可得该矩形从(10,10)开始，至(13,12)为止，正如其坐标所表述的那样。
远嚣 Comment